Exact algorithms for the prediction of optimal structures in
lattice protein models
Several different approaches have been proposed to model protein structure prediction,
which is the problem of predicting the three-dimensional native
structure of a protein given its primary structure. Among these,
one approach of particular interest to us aims at investigating the
prediction of optimal structures using the
simplified lattice model. In
this model, each amino acid is represented as a point in an integer
lattice and the prediction problem is reduced to that of finding the self-avoiding walk(s) of minimum
energy on the lattice. The energy model used here is the HP model, due
to Lau and Dill [1], where one considers the hydrophobic effect as the main
interaction in the folding process. In this model, each amino acid is
encoded as a bead of two different types: Hydrophobic (H) and Polar (or
hydrophilic) (P). Two beads of type H that are topologically
first-neighbours and are not connected in the sequence contribute
negatively to the energy. All the other combinations contribute zero
energy. The protein structure prediction problem on 2D and 3D lattices
is NP complete [2,3].
We have developed an innovative algorithm that outperforms the state of
the art in exact approaches
for 2-D square lattices.
E Giaquinta, L Pozzi: An
effective exact algorithm and a new upper bound for the number of
contacts in the hydrophobic-polar 2D-lattice model. Accepted for Publication. Journal of Computational Biology. Mary Ann Liebert, Inc. Publ.
The algorithm, called minwalk,
is based on a pruned
exhaustive search. The
devised pruning criteria guarantee optimality, while enabling to skip
an exponential number of calls when compared to exhaustive search. The
proposed algorithm can find optimal structures for an input size of up
to around 40-50. Only exact approaches dealing with size up to 25 have
been previously presented in the literature for the 2-D square lattice
[4]. A comprehensive survey of recent results can be found here [7].
Stemming from this result, we envision several directions of research
that we intend to investigate. These directions exploit the
characteristics of the proposed algorithm and are meant to improve and
use its capabilities. They include: adding several missing
optimisations that have the potential to increase the algorithm
efficiency further; extending the algorithm to work on the 3-D cubic
lattice and comparing it to the state of the art [5]; studying
degeneracy in 2-D, beyond the limit of size 25 that has been treated so
far; using the algorithm as a tool to explore the shape of energy
landscapes; exploiting the high parallelism potential of the algorithm
so as to write a parallel version that can take advantage of multi-core
platforms.
The algorithm explores the search space of self-avoiding walks for a
given HP sequence, and its efficiency lies in avoiding exploration of
large parts of such space that are guaranted (by deviced optimal pruing
criteria) not to contain an optimal solution.
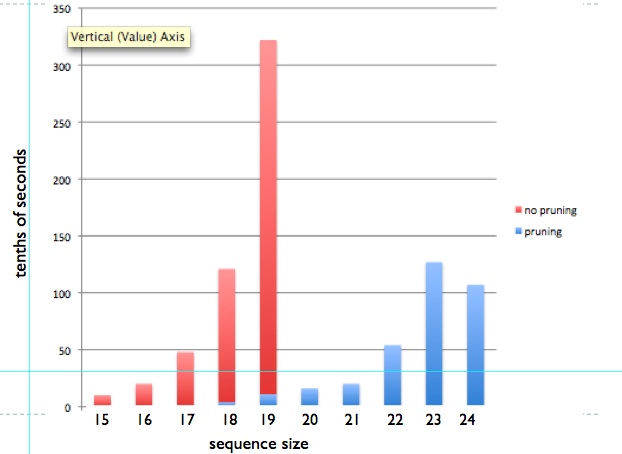
Above, the runtime to find the optimal structure(s) given an input
sequence of a certain size, is shown.
The red bars correspond to an exhaustive search, without pruning
criteria (the complete search space is explored). This method does not
scale and it was only run for sequences up to size 19, in this
experiment. The blue bars correspond instead to a pruned, still
optimal, search. Some simple pruning criteria are implemented, to show
the power of pruning. Only a small fraction of the time is needed
to find the same optimal solution, and sequences of around 25 beads can
be processed optimally in a matter of seconds.
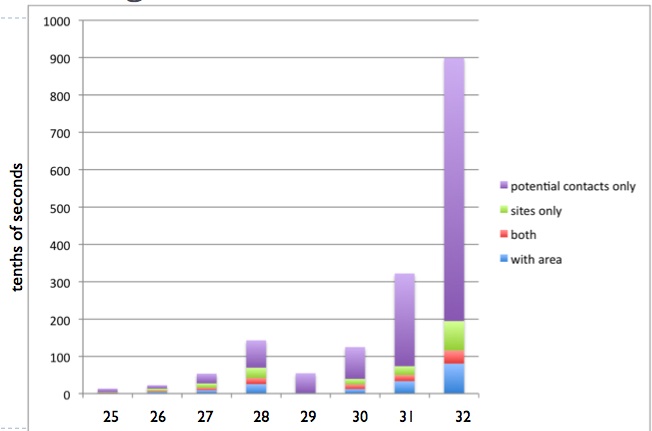
As the project goes on, more and more pruning criteria are devised, and
performance increases exponentially.
At the moment, sequences of length 40-50 can be processed optimally in
a matter of seconds/minutes.
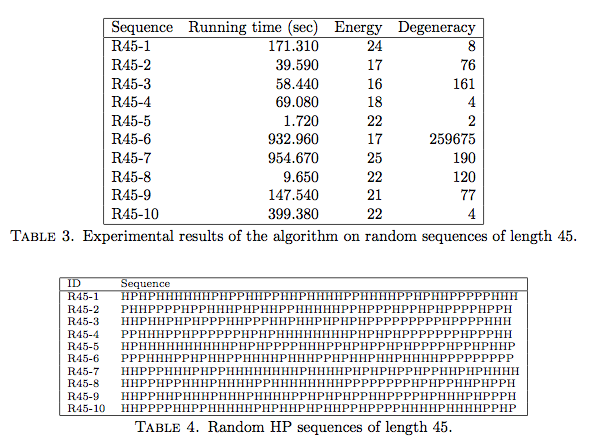
The tables above show some results for random sequences of length 45:
for each sequence, we write the time needed by minwalk to find the optimal
solution(s), the energy of the optimal solutions (number of H-H
contacts) and the degeneracy (number of different solutions with
optimal energy).
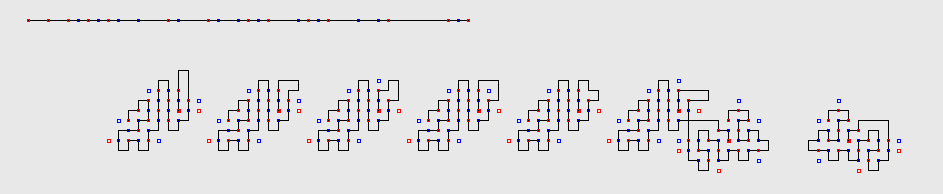
This figure depicts Sequence R45-1 from Table 3 above, and
all its 8 optimal structures of 24 contacts.
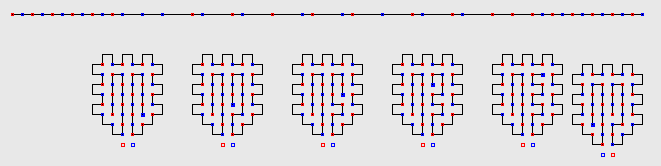
Sequences and structures are depicted thus in the picture: red and blue
squares represent H beads.
P beads are simply depicted as a line without a square.
The red and blue colours are used to distinguish (and quickly
visualise) H beads of even
and odd index (in
the 2D square and 3D cubic lattice, due to the parity issue,
beads of odd index can only create contact with beads of even index and
viceversa).
Several non-optimal approaches have been engineered, in order to deal
with very long HP sequences. In particular, a recent contribution [6]
presents a non-optimal, well performing heuristics approach, and
compares with several previous ones. minwalk
can in some cases detect all optimal
solutions, for a given sequence, faster than all published non-optimal
approaches could.
In particular, for the following benchmark sequence denoted S1-8 in [6]
( H^12 (PH)^2 (P^2 H^2)^2 P^2 H P^2 (H^2 P^2)^2 (HP)^2 H^12 ), of
length 64, the best known result is 42 contacts, and state of the art
heuristics find such structure in running times of the order of hours
to days.
minwalk finds all 39 optimal
structures of 42 contacts in a matter of seconds (six of them are shown
in the figure below).
An exact algorithm such as minwalk,
that is able to return, given an input sequence, all optimal structures
for that sequence—and potentially also all structures for energy levels
close to optimal—can be an interesting tool for providing
insights into the shape of energy landscapes [8].
Exhaustive exploration of the search space of self-avoiding-walks,
without pruning, when in search of an optimal configuration, corresponds
to searching a needle in a haystack, as Levinthal put it in his
argument [9]. In such scenario, all leaves, which correspond to all
possible configurations, might be visited before the optimal
configuration is declared so.
Algorithm pruning, instead, can be seen as a parallel to the reason why
a protein does find its optimal conformation in a reasonable time.
Pruning eliminates an exponential number of weak tree-leaves
(low-contacts configurations), and makes the search more to-the-point.
In other words, it cuts away a section of the haystack, where the
needle certainly is not.
A graphical view of pruning at work is shown below.
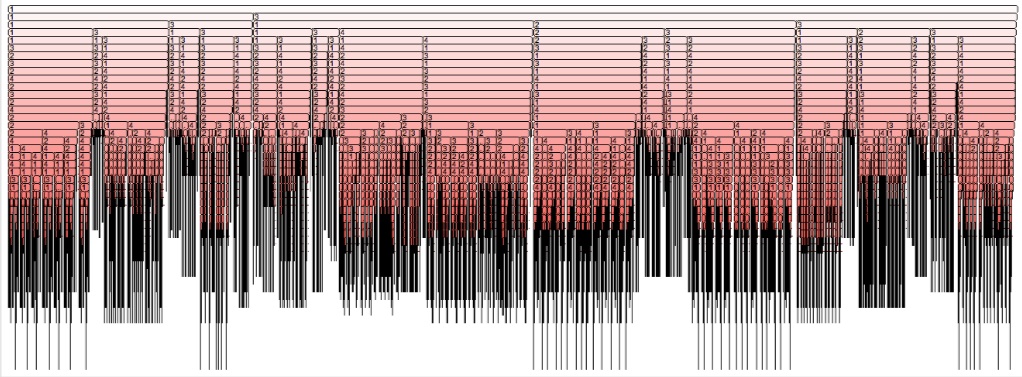
It depicts all recursive calls that minwalk has performed, for a
sequence of length 48 that has several optimal configurations (several
optimal leaves).
Each horizontal line in the figure corresponds to a search-tree level,
and each level expands into different choices (branches of the search
tree). At some specific points, pruning occurs, and all calls from a
specific subtree are dropped. The several leaves explored (black lines
that reach all the way to the bottom of the
tree) correspond to the optimal configurations. No other leave is
explored, and, in most parts of the tree, pruning occurs very early.
If we wrap the pruned tree around, we obtain a funnel, that has some
resemblance to an energy landscape. In this figure, the vertical axis
represents the level of the search tree (the level of each partial
configuration explored), while in an energy landscape the vertical axis
represents energy instead. On the other hand, the pruned partial
configurations (lines that stop high, and do not reach the bottom of the
tree) are those that lead to few-contacts (high energy) structures. The
pruned, high points represent, therefore, high energy configurations—the
same way as in energy funnels.
However, the high energy (non optimal) configurations are not enumerated
(not searched, not visited) in the tree --- visiting them would
correspond to the needle in the haystack again. They are
all ’hidden’ behind the process of pruning.
E Giaquinta, L Pozzi: An
effective exact algorithm and a new upper bound for the number of
contacts in the hydrophobic-polar 2D-lattice model. Accepted for Publication. Journal of Computational Biology. Mary Ann Liebert, Inc. Publ.
[1] Kit Fun Lau and Ken A. Dill. A lattice statistical mechanics model
of the conformational and sequence spaces of proteins.
Macromolecules, 22(10):3986–3997, 1989.
[2] Pierluigi Crescenzi, Deborah Goldman, Christos H. Papadimitriou,
Antonio Piccolboni, and Mihalis Yannakakis. On the complexity of
protein folding. Journal of Computational Biology, 5(3):423–466, 1998.
[3] Bonnie Berger and Frank Thomson Leighton. Protein folding in the
hydrophobic-hydrophilic (HP) model is NP- complete. Journal of
Computational Biology, 5(1):27–40, 1998.
[4] Anders Irback and Carl Troein. Enumerating designing sequences in
the HP model. Journal of Biological Physics, 28(1):1–15, January
2002.
[5] Rolf Backofen and Sebastian Will. A constraint-based approach to
fast and exact structure prediction in three- dimensional protein
models. Journal of Constraints, 11(1):5–30, January 2006.
[6] Alena Shmygelska and Holger Hoos. An ant colony optimisation
algorithm for the 2D and 3D hydrophobic polar protein folding problem.
BMC Bioinformatics, 6(1):30, 2005.
[7] Sorin Istrail and Fumei Lam, Combinatorial Algorithms for Protein
Folding in Lattice Models: A Survey of Mathematical Results. 2009.
[8] Ken A. Dill and Hue Sun Chan. From Levinthal to pathways to
funnels. Nature Structural Biology, 4(1):10–19, 1997.
[9] Cyrus Levinthal. Are there pathways for protein folding? Journal de
Chimie Physique et de Physico-Chimie Biologique, 65:44–45, 1968





